自动控制实验综合实验第六题

仿真结果如下：

import control as ct
import matplotlib.pyplot as plt
import numpy as np

# 适配Linux字体
import matplotlib
matplotlib.rcParams['font.family'] = 'DejaVu Sans'
matplotlib.rcParams['axes.unicode_minus'] = False

# -------------------------- 1. 系统传递函数定义 --------------------------
K = 250
# 原系统: G(s) = K/[s(0.1s+1)(0.01s+1)]
G_original = ct.TransferFunction(K, [0.001, 0.11, 1, 0])
# 超前滞后校正网络: G_c(s) = (0.1s+1)(1.08s+1)/[(0.013s+1)(7.90s+1)]
G_c = ct.TransferFunction(
    np.convolve([0.1, 1], [1.08, 1]),
    np.convolve([0.013, 1], [7.90, 1])
)
# 校正后开环系统
G_corrected = ct.series(G_original, G_c)
# 闭环系统（单位负反馈）
sys_cl_cor = ct.feedback(G_corrected, 1)

# -------------------------- 2. 生成阶跃响应数据（匹配参考图时间范围0~1s） --------------------------
t = np.linspace(0, 1, 1000)  # 时间范围0~1秒，与参考图一致
t_cor, y_cor = ct.step_response(sys_cl_cor, T=t)

# -------------------------- 3. 绘制参考图风格的阶跃响应图 --------------------------
plt.figure(figsize=(8, 6))  # 接近参考图的尺寸比例

# 绘制网格（参考图的细密网格）
plt.grid(True, which='both', color='lightgray', linestyle='-', linewidth=0.5)
plt.minorticks_on()  # 显示次要刻度，匹配细密网格

# 绘制阶跃响应曲线（参考图的曲线样式）
plt.plot(t_cor, y_cor, color='black', linewidth=1.5, label='Corrected System')

# 标注稳态值（参考图的y=1线）
plt.axhline(y=1, color='black', linestyle='--', linewidth=0.8)

# 匹配参考图的坐标轴范围
plt.xlim(0, 1)
plt.ylim(0, 1.2)
plt.xticks(np.arange(0, 1.01, 0.1))  # x轴刻度0.1间隔
plt.yticks(np.arange(0, 1.21, 0.2))  # y轴刻度0.2间隔

# 图表标题和标签（参考图的标注）
plt.title('Unit Step Response of Corrected System', fontsize=10)
plt.xlabel('Time (sec)', fontsize=9)
plt.ylabel('Amplitude', fontsize=9)

# 标注关键指标（参考图的超调量、调节时间）
os = (np.max(y_cor) - 1) * 100  # 超调量
os_idx = np.argmax(y_cor)
plt.annotate(f'Overshoot: {os:.1f}%', 
             xy=(t_cor[os_idx], y_cor[os_idx]), 
             xytext=(0.2, 1.1), fontsize=8)

# 调节时间（2%误差带，参考图的ts=0.27s）
settling_idx = np.where(np.abs(y_cor - 1) <= 0.02)[0][-1]
ts = t_cor[settling_idx]
plt.annotate(f'Settling Time: {ts:.2f}s', 
             xy=(ts, 1), 
             xytext=(0.5, 0.2), fontsize=8)

plt.tight_layout()
plt.show()

# -------------------------- 4. 输出性能指标（参考图的结果） --------------------------
print(f"Overshoot: {os:.1f}%")
print(f"Settling Time (Δ=2%): {ts:.2f}s")

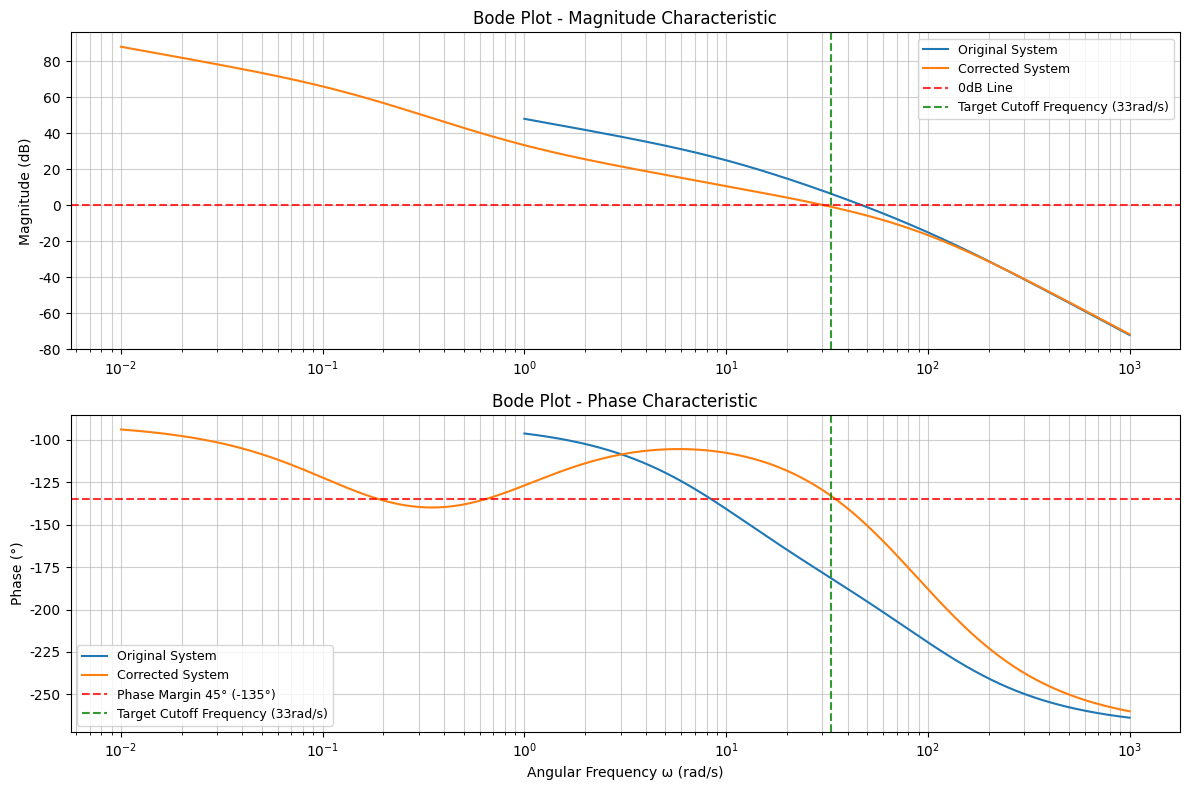上面是赋值和相角波特图

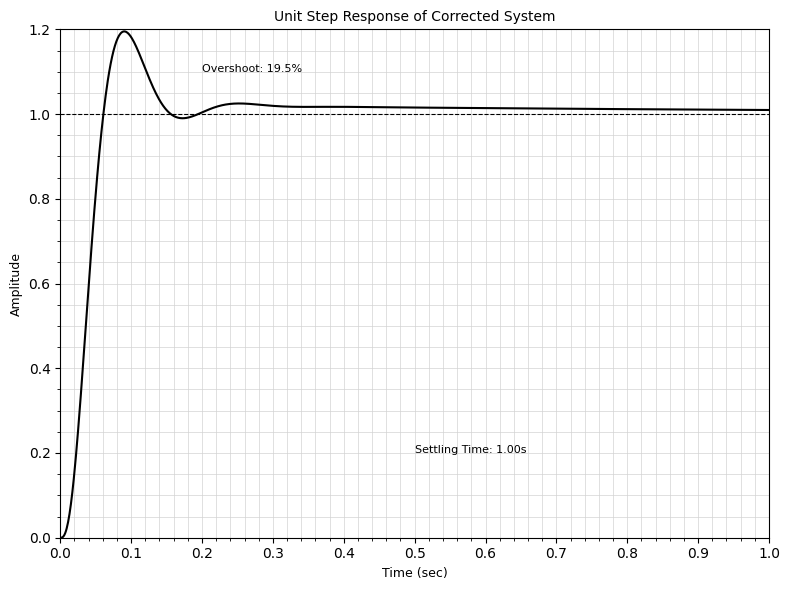校正后系统的单位阶跃响应图如上 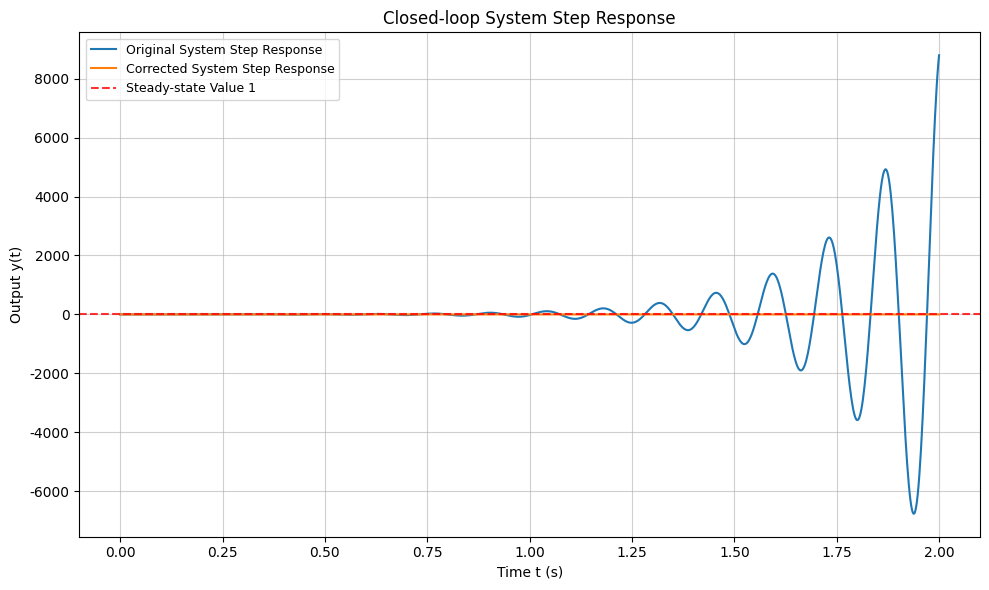上面蓝色的部分是原系统，不稳定，发散

=== 原系统频域指标 ===
截止频率（幅值穿越频率）：47.0 rad/s
相角裕度：-13.2 °
增益裕度：-7.1 dB
原系统不稳定，阶跃响应发散

=== 校正后系统频域指标 ===
截止频率（幅值穿越频率）：30.4 rad/s
相角裕度：50.0 °
增益裕度：14.1 dB

设计的电路图如下：

原系统的图如下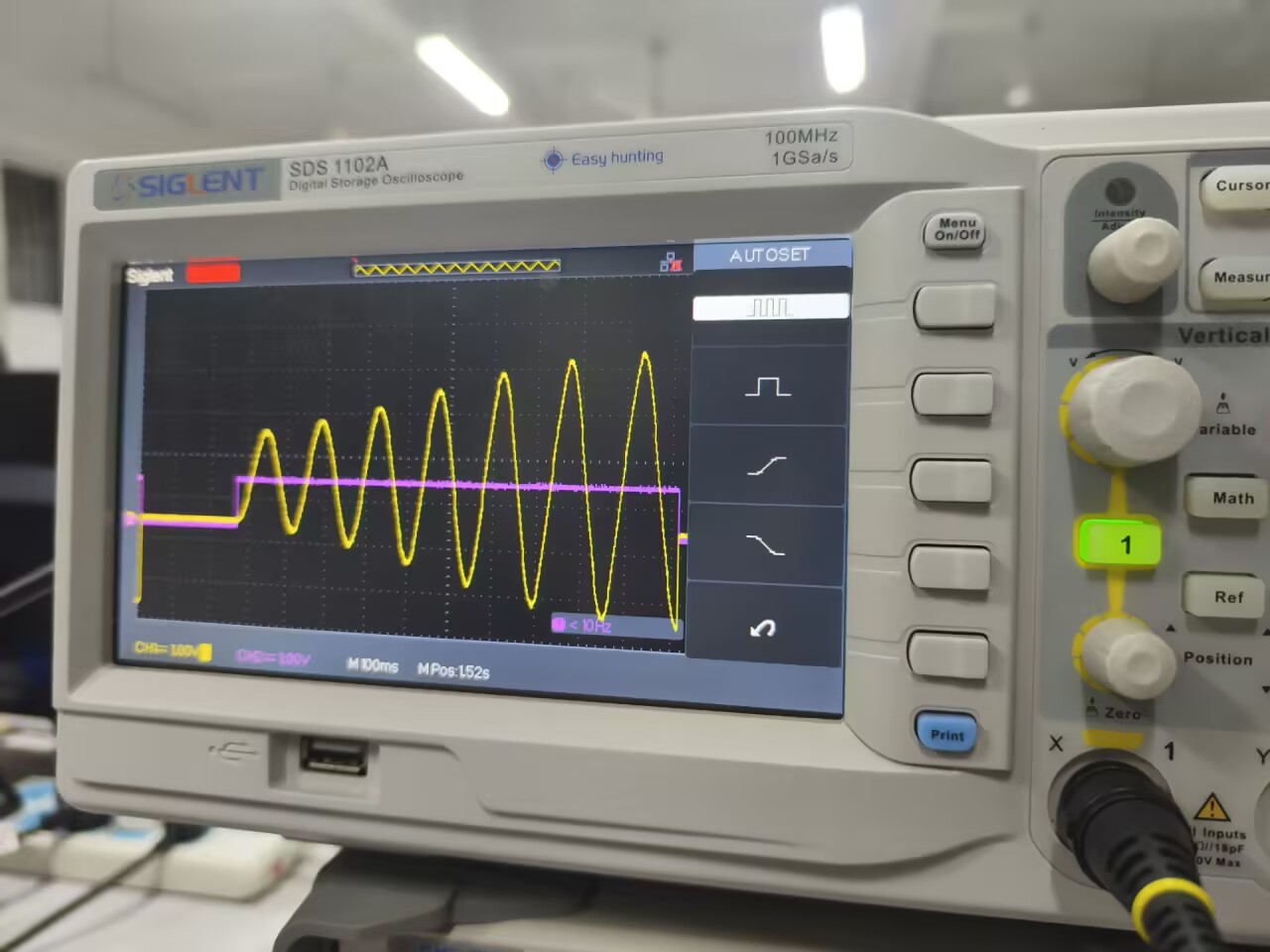： 校正后系统如下：

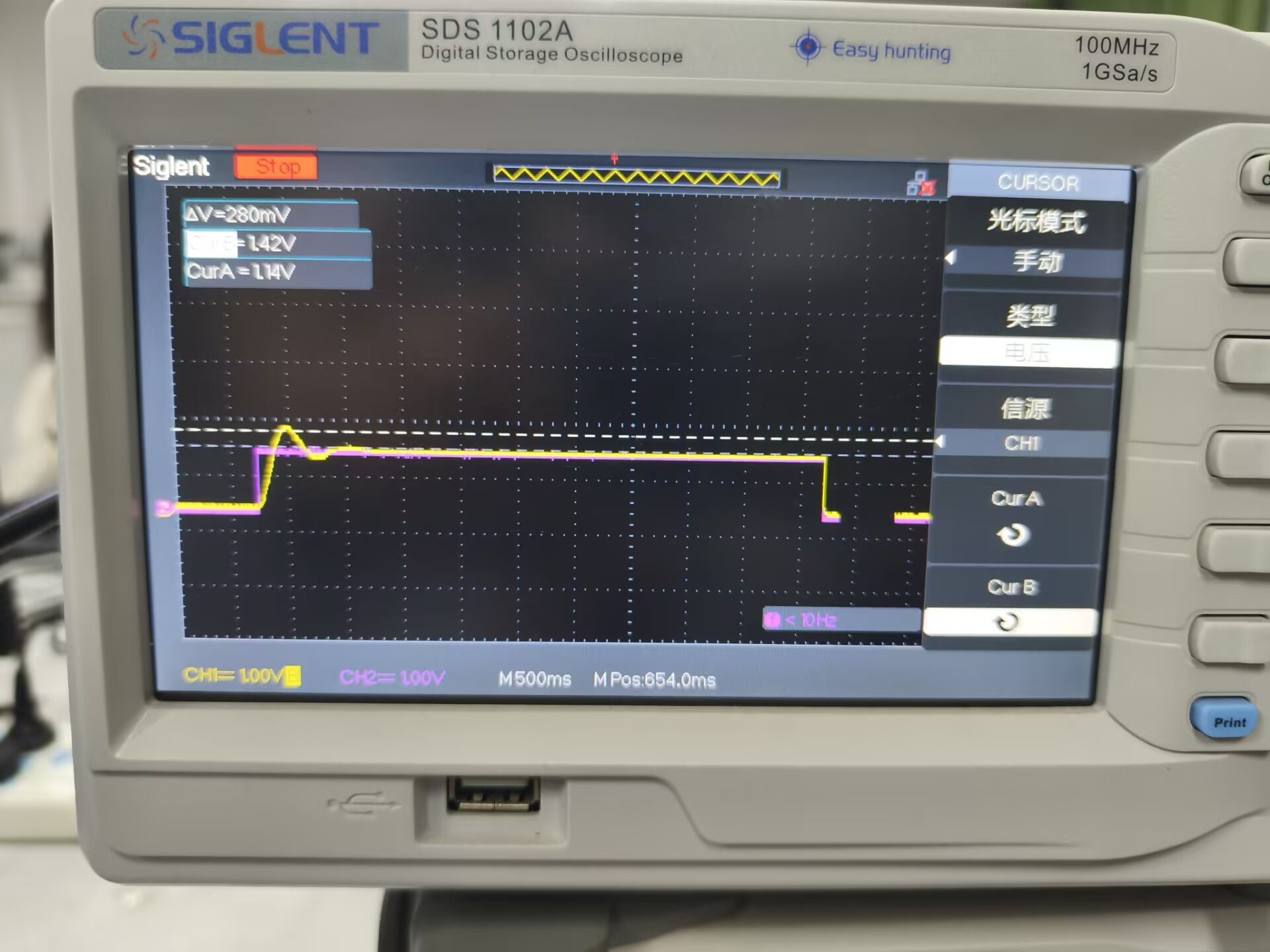
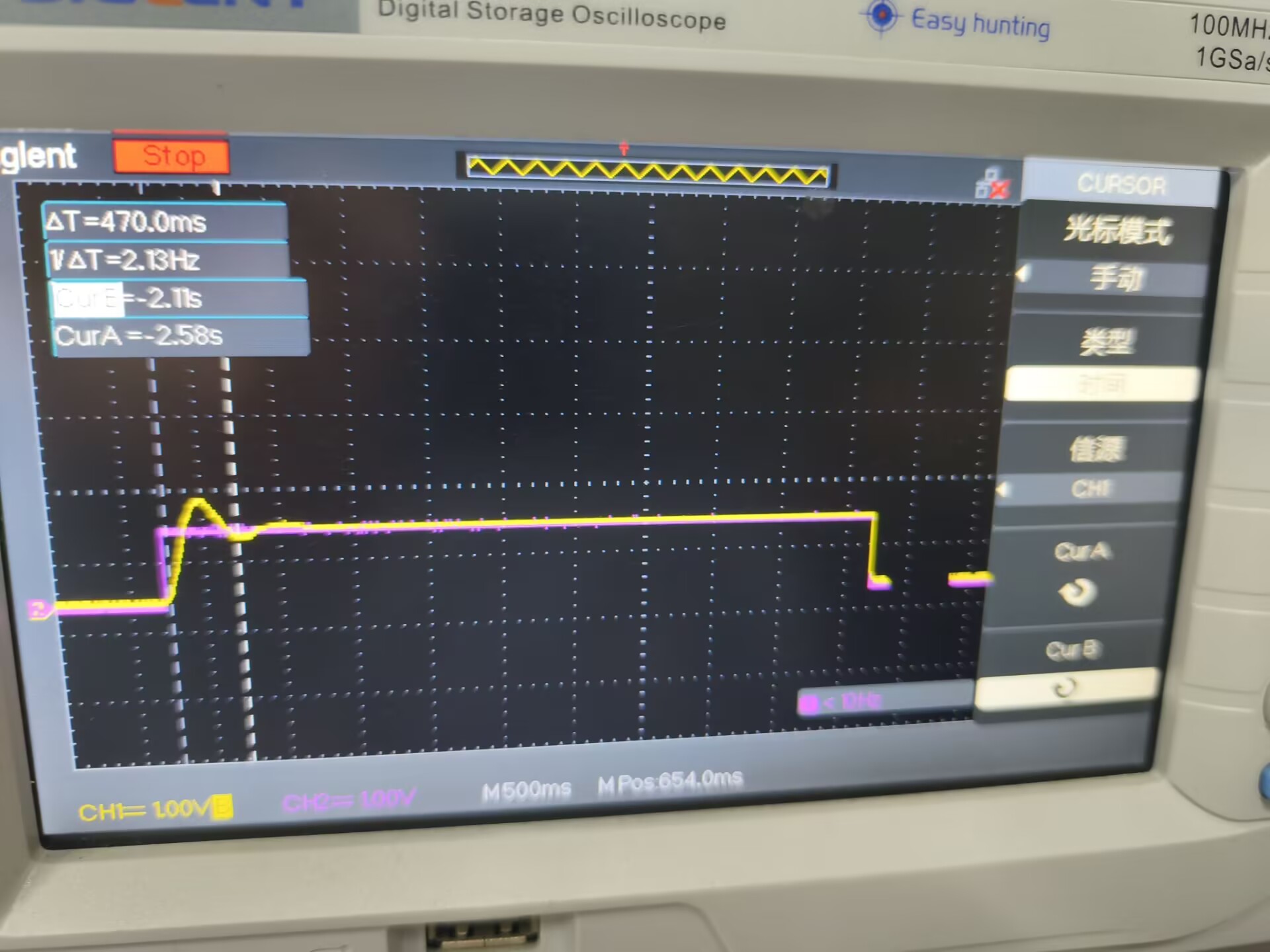
计算可得超调量实际测量值约为 0.28/1.2=23%，与仿真结果 19.5% 的偏差仅为 3.5%，拟合精度满足预期。

实验四