前言

这篇记录学习最优化的各种无约束最优化方法

1.最速下降法

这个就是梯度下降法，用一个步长去乘以Xn的一阶偏导数，算得Xn+1的值，从而不断接近极值点

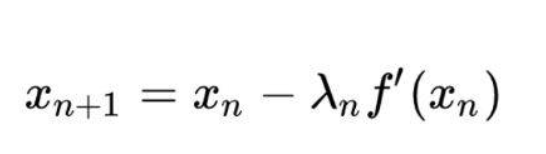
2.牛顿法

牛顿法的基本思想就是用泰勒二阶展开式g（x）来近似代替f（x），当g（x）求得极小值点的时候近似于f（x）的极小值，但是并不是，所以要继续不停的迭代。 二阶导就是海森矩阵

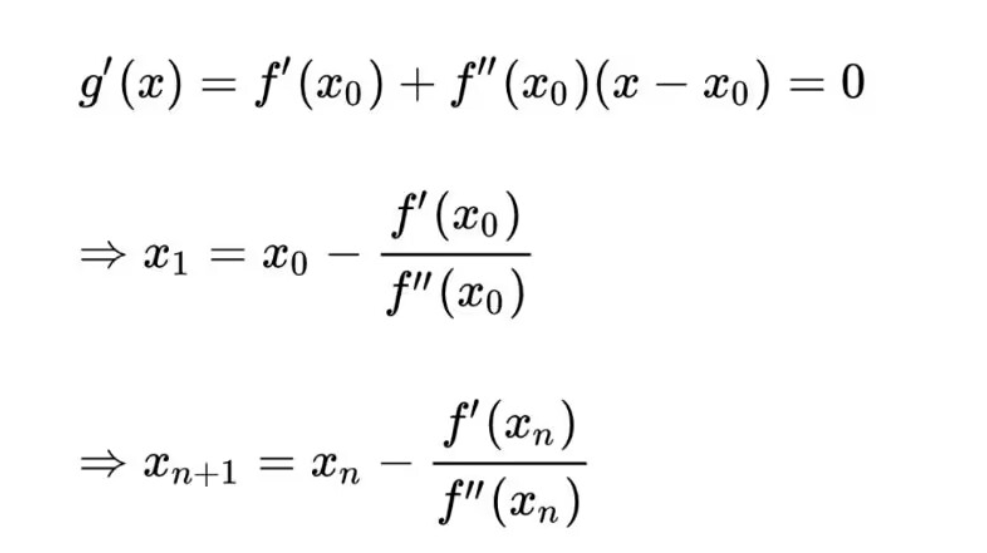
牛顿法与最速下降法的区别在于：最速下降法在下降的时候只去坡度最大的地方去进行迭代（只有1阶导），而牛顿法会在考虑这次下降的基础上考虑之后能否在进行更大的下降（有2阶导），所以牛顿法迭代次数更少，但是每次迭代要花费更多的时间。总时间来看比最速下降法快

3. 共轭梯度法（最优秀）

仅需一阶导数的（残差）信息，但是克服了最速下降法收敛慢的特点，存储低，因为无需存储矩阵，只需要存储少量向量，适用于大规模模型训练

4. 拟牛顿法

DFP 近似海森矩阵的逆

BFGS 近似海森矩阵