第四问：化学成分关联关系分析

问题背景

不同类型的古代玻璃由于其制作工艺、原料配比和历史背景的差异，化学成分之间可能存在不同的关联模式。本问题旨在分析高钾玻璃和铅钡玻璃两种类型玻璃中化学成分间的关联关系，并探讨这些关联关系是否存在显著差异。

1. 研究目标

主要目标：分析不同类型玻璃（高钾玻璃vs铅钡玻璃）中化学成分间的关联关系
具体任务：
1. 构建各类型玻璃的化学成分关联度矩阵
2. 识别关联度差异最大的成分对
3. 验证不同类型间关联关系差异的显著性
4. 可视化分析结果

2. 数据概况

2.1 数据基本信息

总样本数：66个
化学成分数量：14种
玻璃类型分布：
- 高钾玻璃：17个样本
- 铅钡玻璃：49个样本

2.2 化学成分指标

包含14种主要化学成分：

主要成分：二氧化硅(SiO2)、氧化钠(Na2O)、氧化钾(K2O)
次要成分：氧化钙(CaO)、氧化镁(MgO)、氧化铝(Al2O3)
微量成分：氧化铁(Fe2O3)、氧化铜(CuO)、氧化铅(PbO)、氧化钡(BaO)、五氧化二磷(P2O5)、氧化锶(SrO)、氧化锡(SnO2)、二氧化硫(SO2)

3. 模型建立

3.1 灰色关联分析模型

3.1.1 模型原理

灰色关联分析（Grey Relational Analysis, GRA）是一种分析系统中各因素关联程度的多因素统计分析方法，特别适用于样本量较小、信息不完全的系统分析。

3.1.2 核心概念解释

1. 参考序列（母序列）

定义：作为比较基准的数据序列
本研究中：每种化学成分轮流作为参考序列

2. 比较序列（子序列）

定义：与参考序列进行比较的其他数据序列
本研究中：除参考序列外的其他化学成分

3. 关联度

定义：衡量两个序列相似程度的数值指标
取值范围：[0,1]，值越大表示关联性越强

4. 分辨系数（ρ）

定义：用于调节关联系数的参数
作用：提高关联系数的区分能力
本研究取值：ρ = 0.5（常用标准值）

3.1.3 数学模型

步骤1：数据无量纲化处理


对于参考序列 X₀ = {x₀(k)}, k=1,2,...,n
无量纲化： x₀'(k) = x₀(k) / x̄₀

对于比较序列 Xᵢ = {xᵢ(k)}, k=1,2,...,n  
无量纲化： xᵢ'(k) = xᵢ(k) / x̄ᵢ

步骤2：计算关联系数


Δᵢ(k) = |x₀'(k) - xᵢ'(k)|                    (差序列)
Δₘᵢₙ = min min Δᵢ(k)                         (最小差)
      i   k
Δₘₐₓ = max max Δᵢ(k)                         (最大差)
      i   k

ξᵢ(k) = (Δₘᵢₙ + ρ·Δₘₐₓ) / (Δᵢ(k) + ρ·Δₘₐₓ)   (关联系数)

步骤3：计算关联度


γᵢ = (1/n) Σ ξᵢ(k)                           (关联度)
         k=1

3.2 差异显著性检验模型

3.2.1 配对t检验

用于检验两组配对数据的均值是否存在显著差异。

应用场景：比较同一组化学成分对在不同玻璃类型中的关联度差异

假设检验：

H₀：μ₁ = μ₂（两组关联度均值相等）
H₁：μ₁ ≠ μ₂（两组关联度均值不等）

检验统计量：


t = (x̄₁ - x̄₂) / (s_d / √n)

其中：

x̄₁, x̄₂：两组数据的样本均值
s_d：配对差值的标准差
n：样本对数

4. 模型求解过程

4.1 数据预处理

数据加载：读取化学成分数据和玻璃类型信息
数据清洗：处理缺失值和异常值
数据分组：按玻璃类型分为高钾玻璃组和铅钡玻璃组
数据归一化：消除量纲影响

4.2 灰色关联分析计算

4.2.1 分组分析

高钾玻璃组：17个样本的14种化学成分
铅钡玻璃组：49个样本的14种化学成分

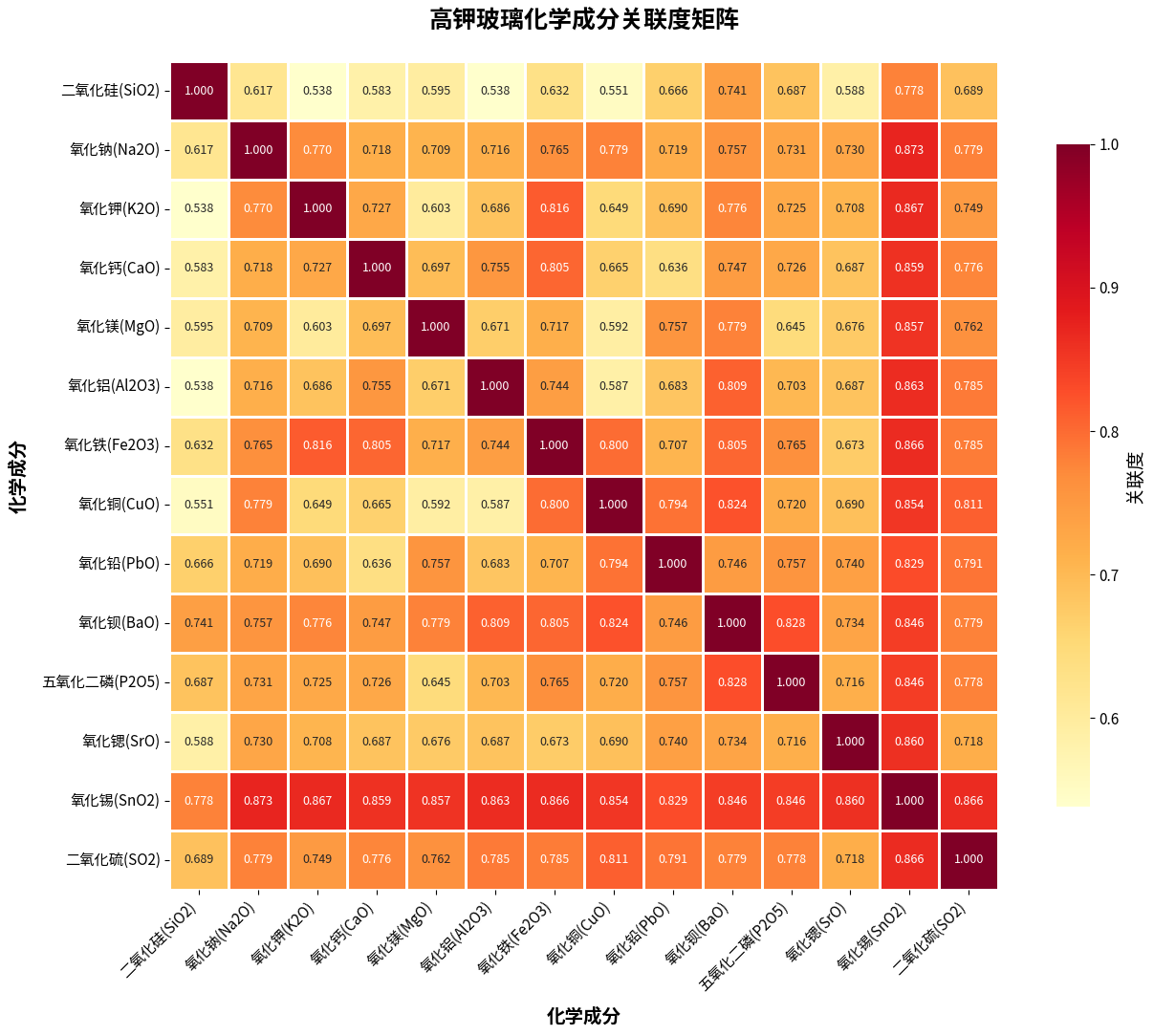
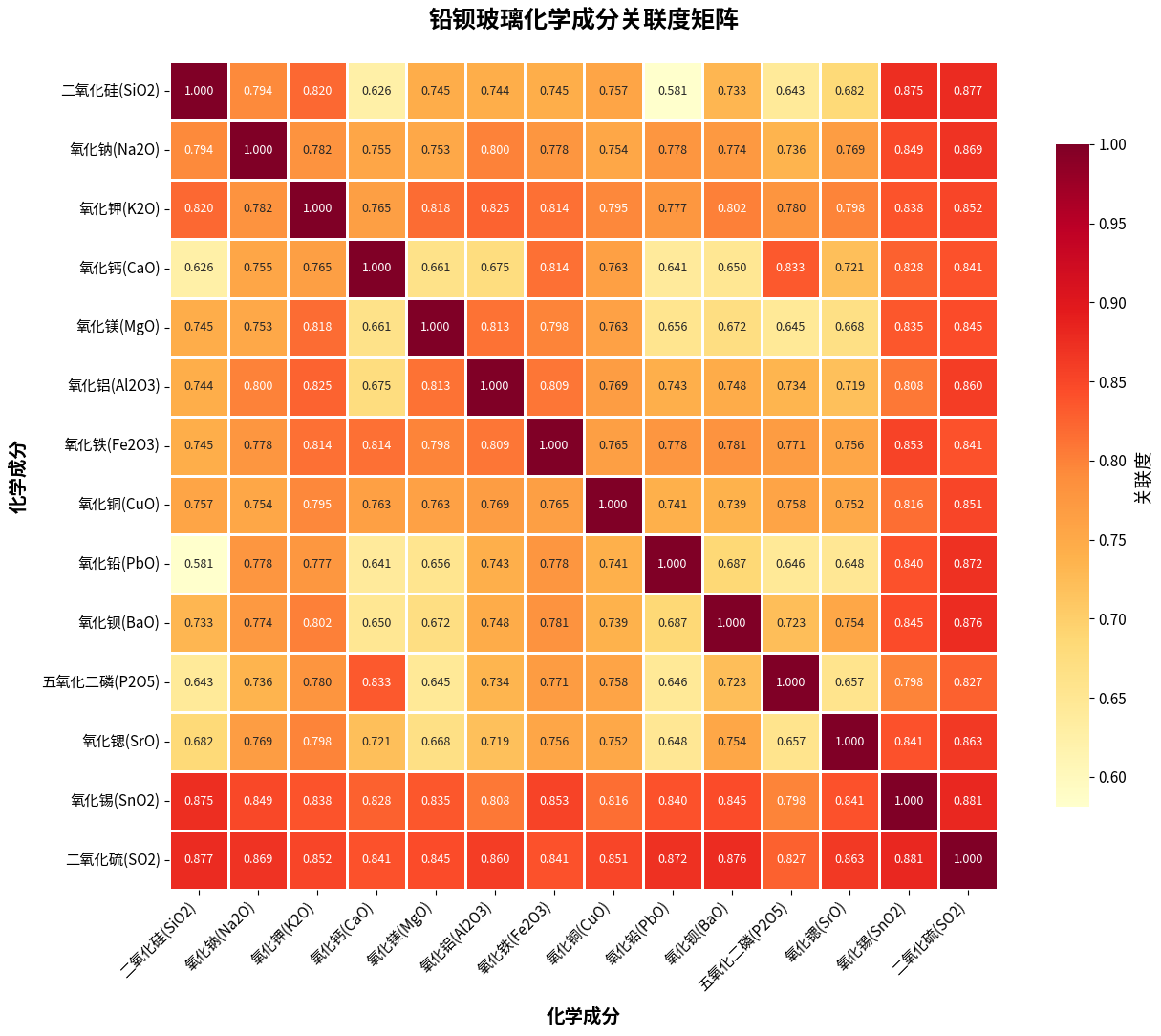
4.2.2 关联度矩阵构建

对每个组别，构建14×14的关联度矩阵：

行：参考序列（14种化学成分）
列：比较序列（14种化学成分）
对角线元素为1（自身关联度）
非对角线元素为计算得到的关联度值

4.3 差异分析

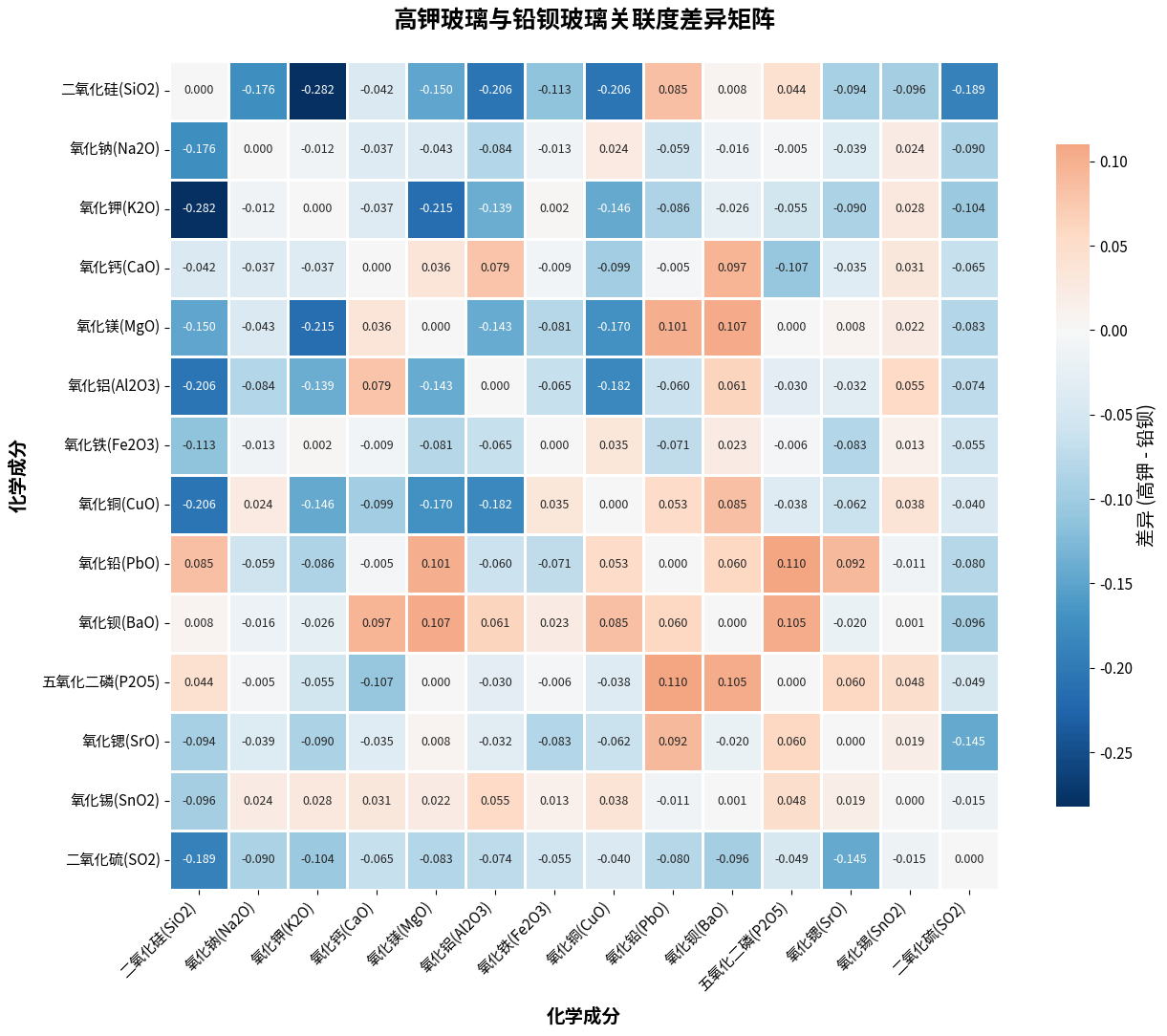
4.3.1 差异矩阵计算


差异矩阵 = 高钾玻璃关联度矩阵 - 铅钡玻璃关联度矩阵

4.3.2 显著差异成分对识别

按差异绝对值大小排序，识别关联关系差异最大的成分对。

5. 主要结果分析

5.1 关联度差异最大的成分对

根据分析结果，关联度差异最大的前10个成分对为：

排名	成分对	高钾关联度	铅钡关联度	差异值
1	二氧化硅(SiO2) ↔ 氧化钾(K2O)	0.5381	0.8205	0.2824
2	氧化钾(K2O) ↔ 氧化镁(MgO)	0.6027	0.8177	0.2149
3	二氧化硅(SiO2) ↔ 氧化铝(Al2O3)	0.5382	0.7439	0.2057
4	二氧化硅(SiO2) ↔ 氧化铜(CuO)	0.5512	0.7568	0.2055
5	二氧化硅(SiO2) ↔ 二氧化硫(SO2)	0.6885	0.8773	0.1888

5.2 显著性检验结果

配对t检验结果：

统计量：t = -5.9141
p值：p < 0.000001
结论：在α = 0.05显著性水平下，拒绝原假设，认为不同类别间的关联关系存在显著差异

5.3 结果解释

5.3.1 主要发现

二氧化硅-氧化钾关联性差异最大
- 在铅钡玻璃中，二氧化硅与氧化钾呈现强关联(0.8205)
- 在高钾玻璃中，两者关联性较弱(0.5381)
- 差异达到0.2824，表明不同类型玻璃的制作工艺存在本质差异
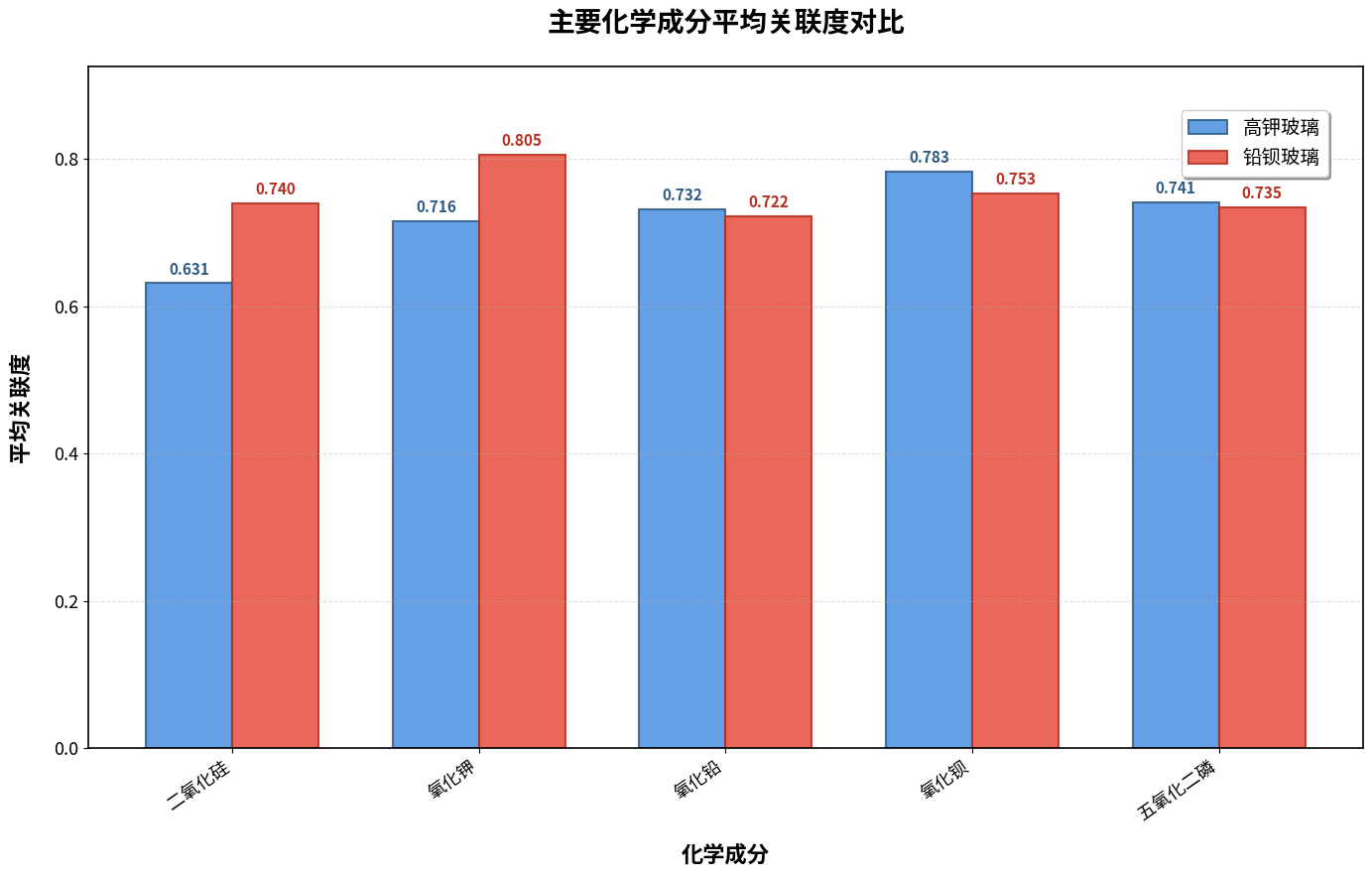
铅钡玻璃化学成分关联性普遍更强
- 大多数成分对在铅钡玻璃中的关联度高于高钾玻璃
- 这可能反映了铅钡玻璃制作工艺的标准化程度更高
高钾玻璃成分关联性相对较弱
- 表明高钾玻璃的制作可能受到更多因素影响
- 或者制作工艺的变异性更大

5.3.2 工艺学解释

制作工艺差异：
- 铅钡玻璃：采用铅、钡化合物作为助熔剂，工艺相对固定
- 高钾玻璃：使用植物灰作为助熔剂，原料组成变化较大
历史背景影响：
- 不同时期、不同地区的制作技术可能存在差异
- 原料来源和加工方式的变化影响成分关联模式

6. 模型优缺点分析

6.1 模型优点

适用性强：灰色关联分析对样本量要求不高，适合本研究的小样本情况
直观性好：关联度矩阵能直观展示成分间的关联强度
稳健性强：对数据分布要求不严格，适合处理非正态分布数据
解释性强：结果具有明确的物理意义和工艺学解释

6.2 模型局限性

线性假设：假设变量间关系为线性，可能忽略非线性关联
权重设定：分辨系数的选择可能影响结果
因果关系：只能反映关联性，无法确定因果关系
动态性缺失：未考虑时间序列特征

7. 结论与建议

7.1 主要结论

显著差异存在：统计检验证实不同类型玻璃的化学成分关联关系存在显著差异
模式差异明显：铅钡玻璃的成分关联性普遍强于高钾玻璃
工艺特征反映：关联模式差异反映了古代玻璃制作工艺的本质差异

7.2 实际意义

文物鉴定：可作为古代玻璃类型判别的重要依据
工艺研究：为研究古代玻璃制作技术提供量化证据
保护策略：为不同类型玻璃文物的保护提供科学依据

7.3 后续研究建议

扩大样本：增加样本量以提高结果的可靠性
引入更多方法：结合主成分分析、聚类分析等多种方法
考虑时空因素：分析不同时期和地区的差异
深入机理研究：从材料科学角度深入分析成分关联的物理化学机理

目录