考试第三题

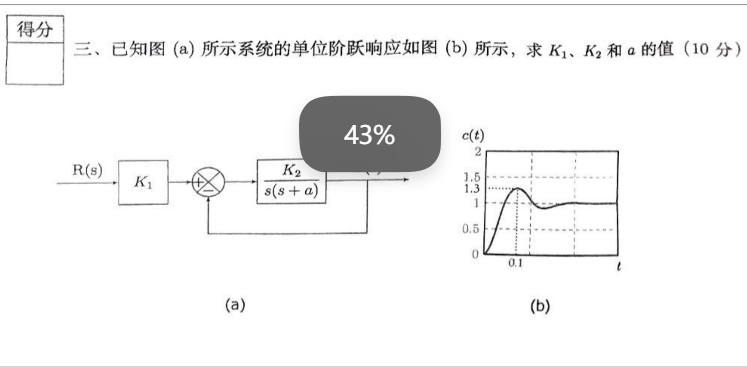
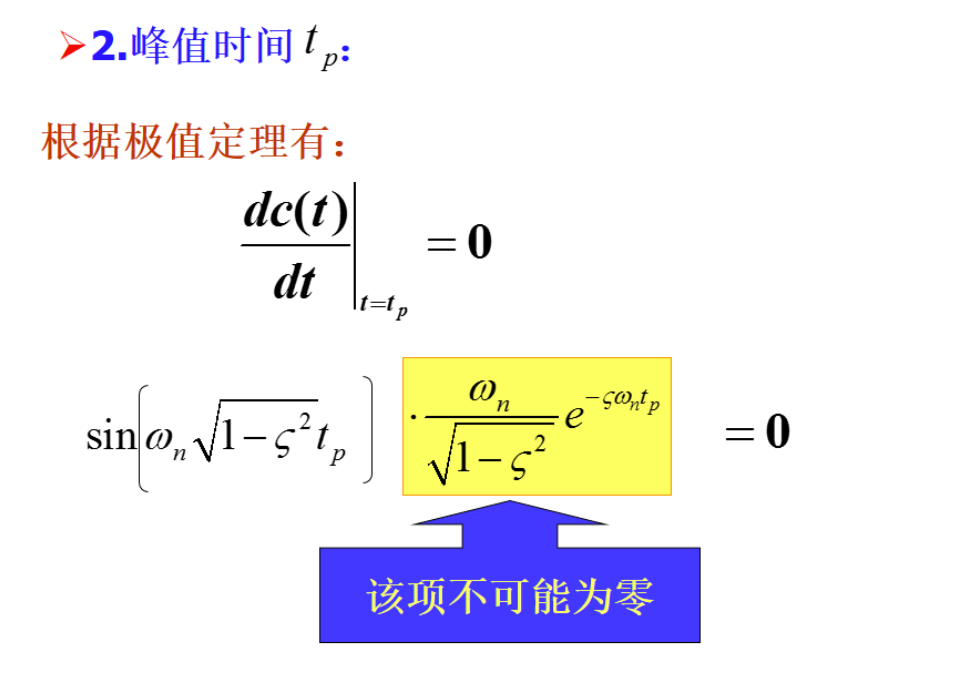
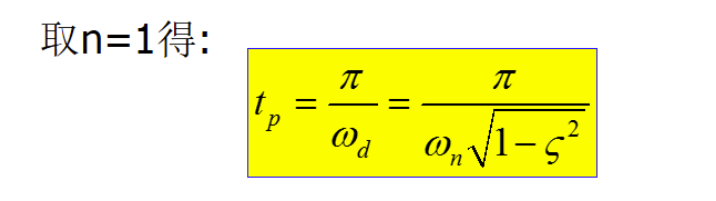
第四题

1. 列劳斯表。劳斯表能解决2个问题：1.求系统稳不稳定，或者求当系统稳定时k的范围。2. 判断正实部根的个数

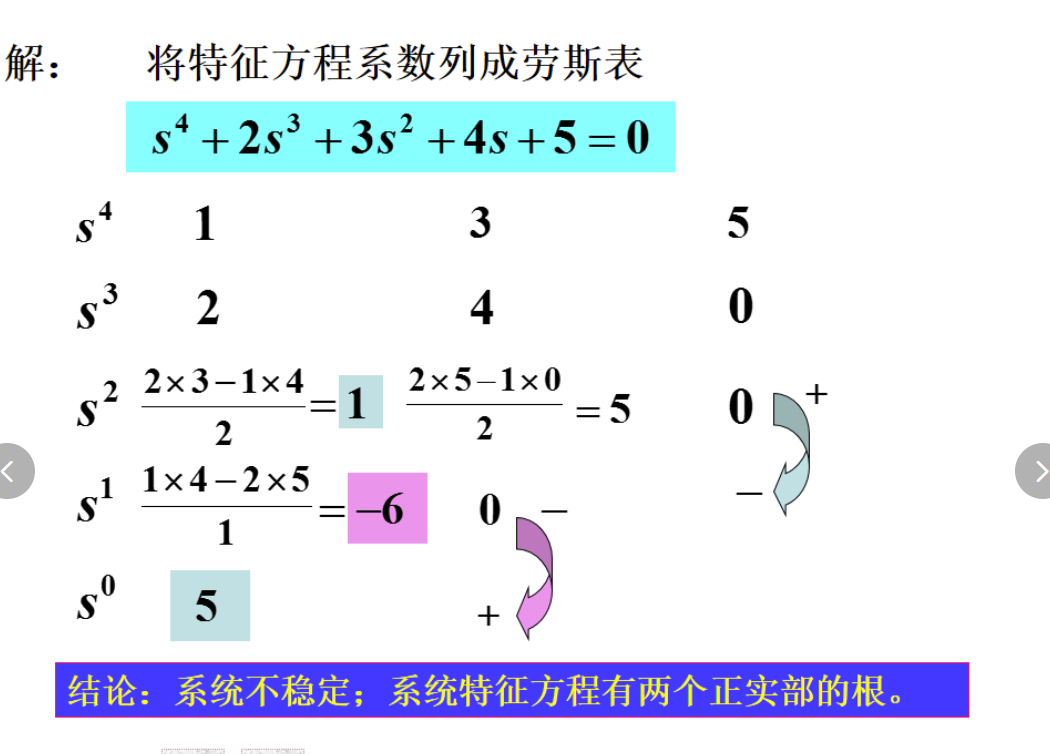
2. 求稳态误差ess。 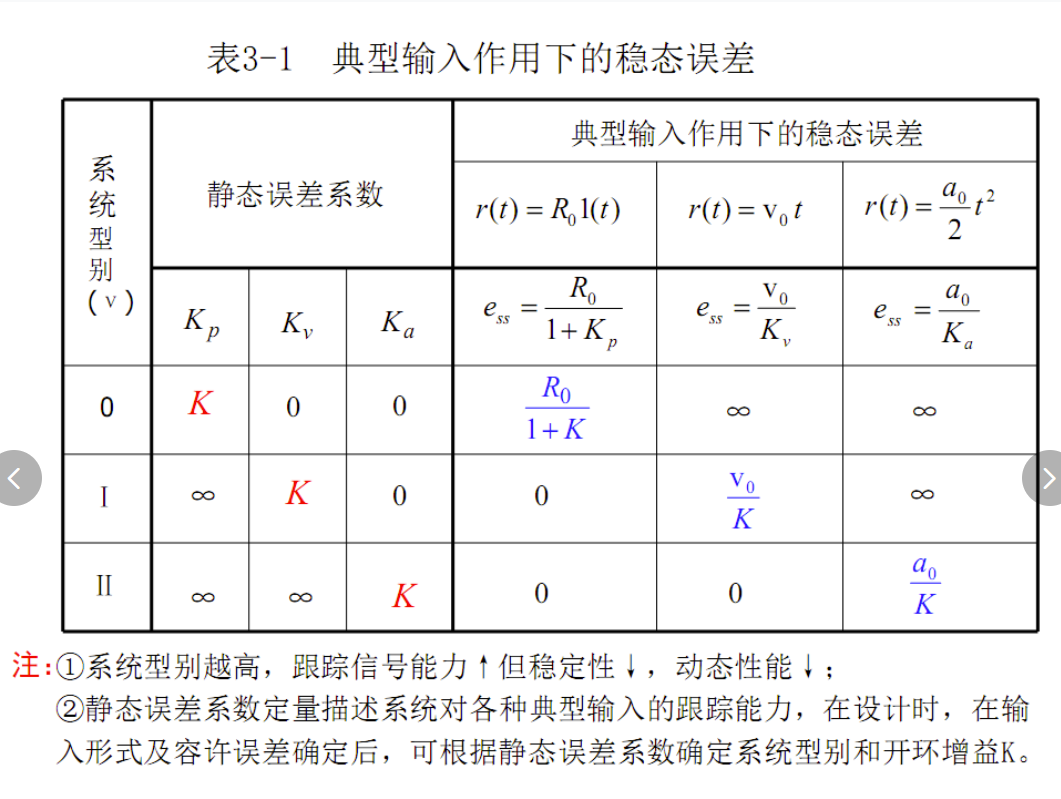判断系统是几型系统，$K_p,K_v,K_a = \lim_{s \to 0} s^v G(s)H(s)$其中v=0，1，2，代表系统的型级。当系统的型级低于输入时，系统无法跟上输入，故误差为无穷大，就像手枪不能打长距离一样，误差就会无限大，同理，当系统的型级大于输入时，误差就为0。当型级和输入相等，就需要套公式算。

第五题：绘制根轨迹

根轨迹就是通过分析特征方程的根的轨迹分布，进而求出一些指标，方便我们进行系统的分析

根轨迹规则

1. 根轨迹分支数 = max(m,n)，通常情况下为开环极点个数n
2. 规则2：根轨迹的每一条分支都是连续的；根轨迹对称于实轴。
3. 当s = 开环极点的时候，根等于0，所以根轨迹始于开环极点。
4. 渐近线把复平面分成了n-m份$\varphi_a = \frac{(2k + 1)180^\circ}{n - m}$其中：$k = 0, \pm1, \pm2, \cdots$
5. 规则5：实轴上的开环零、极点把实轴分为若干个区段，若某段右边的开环零、极点数目之和为奇数，则该段就是根轨迹；否则不是。

6. 规则6：重根点坐标$d$满足方程：$\sum_{j=1}^{n} \frac{1}{d - p_j} = \sum_{i=1}^{m} \frac{1}{d - z_i}$

7. 当要求根轨迹和虚轴的交点坐标时，直接将s = jw代入特征方程，接触w和k的值

频域分析法